이 문제의 조건은 두 가지이다.
① 이웃한 집과의 색은 달라야 한다.
② 첫 번째 집과 마지막 집의 색은 달라야 한다.
예시를 이용해 살펴보기
첫 번째 조건은 전형적인 DP로 해결할 수 있지만, 두 번째 조건은 조금 다른 방식으로 체크해줘야 한다.
문제의 예시에서
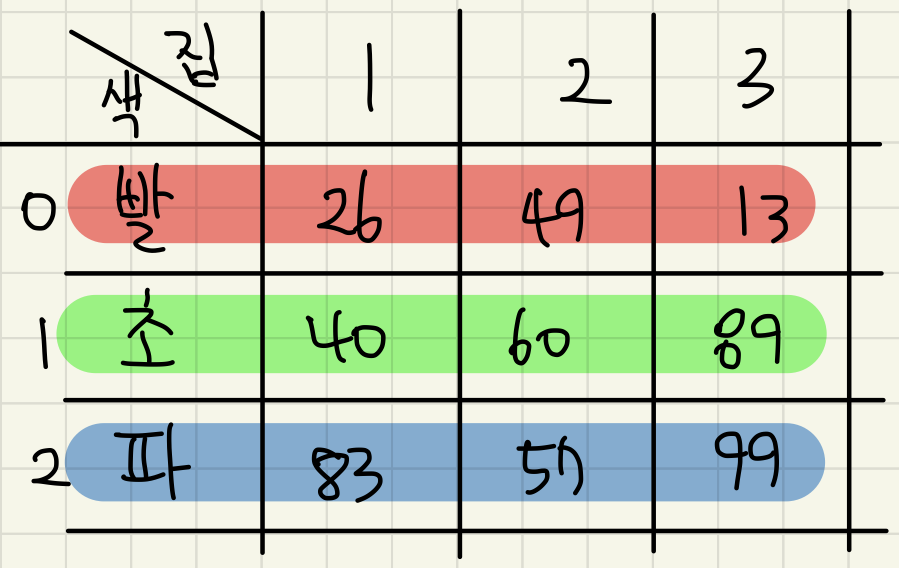
① 번 조건만 생각해 봤을 때에는,
D[i][j] : i번째 집을 j색으로 칠한다고 했을 때 비용의 최솟값,
a[i][j] : i번째 집을 j색으로 칠했을 때의 비용일 때

점화식은 D[i][j]=min(D[i-1][(j+1)%3], D[i-1][(j+2)%3]) + a[i][j] 이다.
여기에서 (j+1)%3, (j+2)%3의 표현은 j와는 다른 색을 선택한다는 의미이다.

이렇게 구한 D[n][0], D[n][1], D[n][2]값들의 최솟값이 답이 된다.
즉, n번째에 칠한 색(j)에 따른 비용의 최솟값(D[n][j])들을 비교하여 그중 가장 작은 비용이 답이 된다.
위의 예시에서는 D[n][0]=96, D[n][1]=172, D[n][2]=185가 되어,
D[n][0]이 답이 된다. 즉, 마지막 n번째 집에 빨간색을 칠했을 경우의 비용의 최솟값이 다른 색을 칠했을 경우와 비교해 가장 작다는 뜻이다.
문제풀이의 Key
여기에서 ②번의 조건을 추가한다면, 첫 번째 선택한 색과 마지막의 선택한 색을 비교해서 같으면 선택하지 못하게 해야 한다.
우리가 구하는 정답은 비용의 최솟값이다.
첫 번째 색이 k라고 하고, D [n][k](n번째 집에 k색을 칠할 때 비용의 최솟값)에 매우 큰 값을 넣는다면
마지막에 저절로 답에서 제외될 것이다.
위의 방법이 이 풀이의 핵심이다.
해결
첫 번째에 선택한 색을 k라고 두고,
위에 서술해놓은 이 풀이의 핵심 key를 사용하여
첫 번째 집에 k가 아닌 색의 비용을 1000*1000이라 하고,
마지막 집에 k인 색의 비용을 1000*1000이라고 한다.

위와 같은 방법으로 k=0~2까지 순회하면서 k값에 따른 문제의 최솟값을 구한 뒤,
모든 최솟값을 비교해 그중 가장 작은 비용을 선택하면 해결된다.
코드
#include <bits/stdc++.h>
#define MAX 1000
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int n;
int a[MAX+1][3]={0,}, d[MAX+1][3]={0,};
cin>>n;
for(int i=1; i<=n; i++){
for(int j=0; j<3; j++){
cin>>a[i][j];
}
}
int res=1000*1000;
for(int k=0; k<3; k++){
// 첫번째집을 k로 선택하는 경우
//cout<<k<<'\n';
for(int i=1; i<=n; i++){
for(int j=0; j<3; j++){
d[i][j]=min(d[i-1][(j+1)%3],d[i-1][(j+2)%3])+a[i][j];
if(i==1){
d[i][j] = 1000*1000;
if(j==k) d[i][j]=a[i][j];
}else if(i==n && j==k){
d[i][j] = 1000*1000;
}
//cout<<d[i][j]<<' ';
}
//cout<<'\n';
}
for(int j=0; j<3; j++){
res=min(res, d[n][j]);
}
}
cout<<res;
return 0;
}
'프로그래밍 > PS' 카테고리의 다른 글
| [백준 12904] A와 B (0) | 2021.05.28 |
|---|---|
| [백준 2109] 순회강연 (0) | 2021.05.26 |
| [백준 14500] 테트로미노 (0) | 2021.03.25 |
| [백준] 골드V 달성 (0) | 2021.03.24 |
| [백준 2133번] 타일채우기 (0) | 2021.03.18 |





































